반응형
집약형 생산함수(intencive from production function)은 콥-다그라스형 1차 동차생산함수의 양변을 노동량(L)으로 나누어서 노동 1인당 산출고를 노동 1인당 자본장비율(K/L) 함수로 나타낸 생산함수를 말한다.
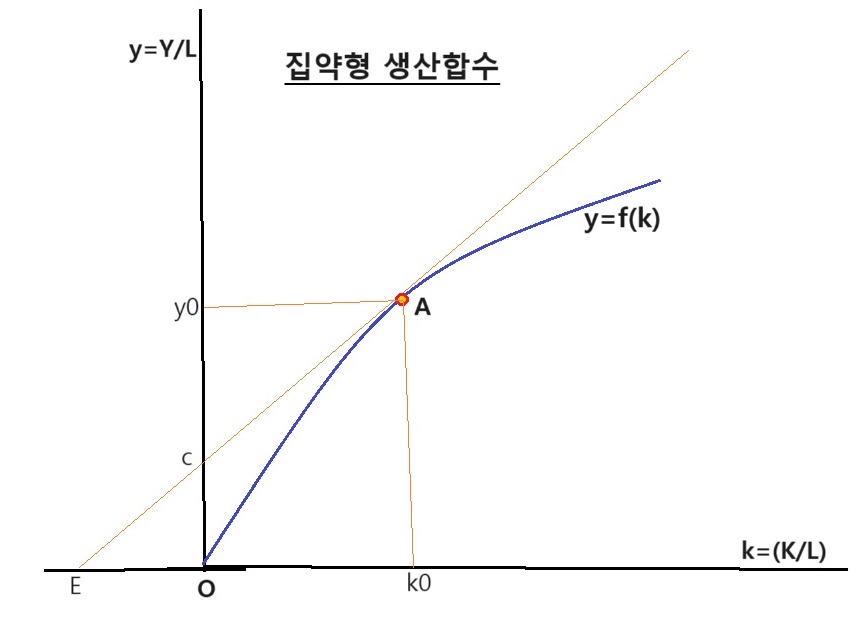
즉 Y=F(L, K) 이를 노동량(L)로 나누면 Y/L=F(1, K/L)이 된다. 이는 노동 1인당 산출고(y=Y/L)가 노동 1인당 자본장비(k=K/L)의 함수로 표시된다. 다시 정리하면 y=f(k) 가 된다.
y=f(k)곡선은 우하향하면서 그 기울기가 점차로 체감한다. 즉 1인당 자본량 k 가 증대함에 따라 1인당 산출고 y도 증가한다. y=f(k)곡선의 기울기는 자본의 한계생산력(MP)을 표시한다. 그 이유는 다음과 같다.

반응형
'경제지식 > 미시경제학' 카테고리의 다른 글
| 제약조건 하의 생산 극대화! 라그랑주 승수를 이용한 생산자균형이론의 수리적 전개! [이춘근 미시경제학 티스토리 109회] (7) | 2023.12.11 |
|---|---|
| CES 생산함수(고정대체탄력성 생산함수)와 VES(변량대체탄력성 생산함수)의 의미와 특징은? [이춘근교수 미시경제학 티스토리 98회] (11) | 2023.12.03 |
| 오일러의 정리와 1차 동차 생산함수! [이춘근교수 미시경제학 티스토리 90회] (12) | 2023.11.28 |
| 콥-더글라스 생산함수(Cobb-Douglas Production Function)의 의미와 속성! [이춘근교수 미시경제학 티스토리 89회] (32) | 2023.11.27 |
| 소비함수에서 소비자잉여 크기 수식 계산 사례! [이춘근교수 미시경제학 티스토리 79회] (0) | 2023.11.17 |