산업연관표 승수효과의 요인 분해방법! [이춘근교수 산업연관분석 티스토리 63회]

국제산업연관표를 이용하여 승수효과의 분해를 설명하면 다음과 같다. 두 지역이나 두 국가(r과 s)가 존재한다고 가정하고, r지역에서 생산되는 섬유제품에 대한 수요가 증가(예를 들어 1,000대)했다고 하자. 그렇다면, r지역의 섬유산업은 섬유제품을 생산하기 위해, 섬유부품(예: 원사, 원면, 염색 등)이나 원재료(예: 전력, 석유 등)을 각 산업으로부터 구입한다. 이 때 r지역의 산업이 부품이나 원재료를 r지역뿐만 아니라 s지역의 산업으로부터도 구입하게 되면, s지역의 산업 생산도 유발되게 된다.

r지역의 산업에 있어 직접・간접적으로 r지역에 유발되는 생산은 「지역내 승수효과(intra-regional multiplier effct)라고 하며, r지역의 산업에 의한 수요를 충족하기 위해 s지역의 산업에 있어 직접 및 간접 유발되는 생산은 「지역간 확산효과(interregional spillover effect)」라고 한다. 또한 r지역으로부터의 수요에 의해 초래되는 s지역의 산업생산의 증가는, 산업 간의 관계를 통해 s지역의 산업으로부터 다시 r지역의 산업에 대한 수요도 유발한다. 그로 인해, r지역의 산업 생산이 다시 유발된다. 이와 같이, r지역에서 발생한 섬유제품에 대한 수요의 증가가, s지역에 있어서의 산업의 생산을 유발하는 것을 통해, 다시 r지역의 산업 생산이 유발되는 효과를「지역간 환류(또는 피드백) 효과」(interregional feedback effect)라 한다. 즉, 지역간의 승수효과는, 「지역내 승수효과」, 「지역간 스필오버 효과」 및 「지역간 피드백 효과」의 3개로 나누어 생각할 수 있다(표 1 참조).

 

승수효과	의미
지역내(Intra-regional) 승수(Multiplier)효과	자기지역(또는 국가) 최종수요에 의해 자기지역(국가)의 산업에 직접 및 간접으로 유발되는 생산효과
지역간(Inter-regional) 확산(Spillover)효과	자기지역(또는 국가)에서 발생한 최종수요를 만족하기 위해 직접 및 간접으로 유발되는 타 지역(국가)의 생산효과 (어느 국가(또는 지역)의 생산이 다른 국가의 생산을 유발하는 효과)
지역간(Inter-regional) 피드백(Feedback)효과	자기 지역(또는 국가)에서 발생한 최종수요를 만족하기 위해 유발된 타 지역(국가)의 산업에 의해, 다시 자기지역에 유발되는 생산효과 (어느 국가의 생산이 다른 국가에 파급되고, 다시 자국에 유발되는 효과)

 

이와 같이, 어느 지역의 산업에 대해서 발생한 수요에 의해 직접 및 간접적으로 유발된 생산을, 지역간의 거래에 유의하여 분류하는 시도가 「승수 분해」이다. 이것들의 각 효과를 도식화한 것이 <그림 1>이다.

 

 

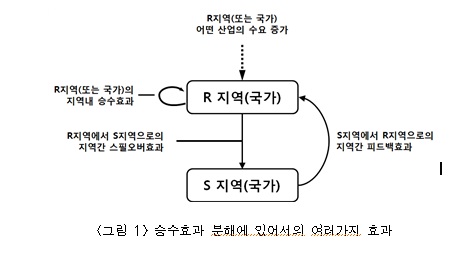
승수효과를 상기 3개로 분해하는 것은 국가간 또는 지역간의 산업연관구조에 관한 특징을 분명히 구분할 수 있기 때문이다. 먼저, 지역내 승수효과의 크기는 지역내에서 발생한 수요를 자기 지역내의 산업이 어느 정도 충족할 수 있는가 하는 지역내 산업의 파급효과를 나타내는 지표가 될 수 있다(다시 말하면, 국내 승수효과는 자기 지역의 산업기반의 「힘」 혹은 「충실도」를 나타내는 지표라 할 수 있다).

반면에, 지역간 스필오버 효과의 크기는, 자기 지역과 타지역의 산업과의 분업 정도를 나타내는 지표로서의 역할을 한다. 지역간 피드백 효과의 크기는 자기 지역과 타지역 간 행해지는 분업이 어느 정도 중층적으로 행해지고 있는지를 나타내는 지표로서의 역할을 한다.

다음으로, Miller(1966), Round(1985, 2001) 및 Miller and Blair(2009) 등의 연구를 참고하여 가장 간단한 2개 지역(또는 국가)에 적용가능한 승수 분해방법을 살펴보고자 한다. 이는 국제산업연관표와 같이 보다 많은 국가가 존재하는 경우에도 적용될 수 있다.

그러나, 지역의 수가 3개지역 이상으로 증가하면, Round(1985)외 와 Stone(1985)에서 행해진 것 같은 승수의 엄밀한 분해는 곤란해진다. Round(1985)는 3개 지역 경우에 승수 분해가 가능한 방법을 설명하였지만, 3개 지역 이상의 경우에는, 2개 지역 모형에 있어서의 같은(Round(1985)외나 Stone(1985)과 같이) 국가간 스필오버효과나 피드백효과를 계산하기가 곤란하다고 지적되고 있다(Round(1985, pp. 397-398) 참조).

 

반응형

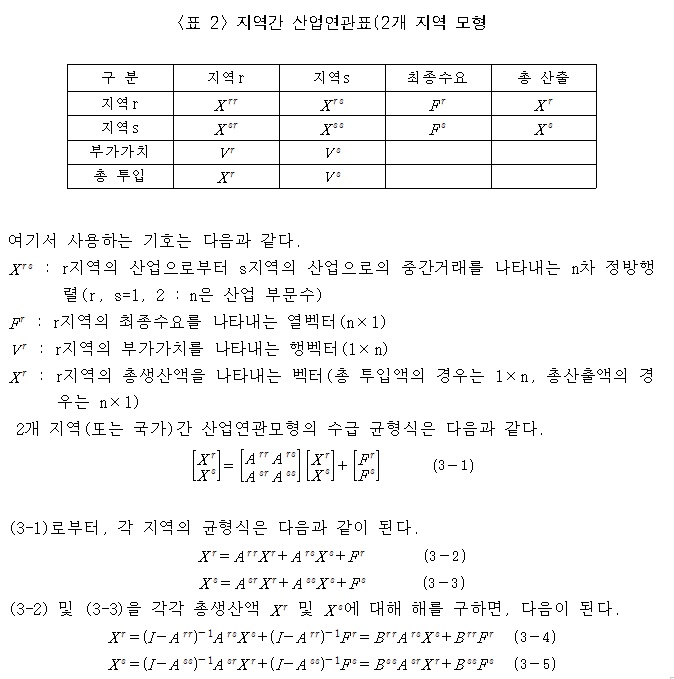
r과 s의 두 지역간의 적용가능한 간단한 지역간 산업연관모델을 가정하여 설명하면 다음과 같다.